Show Attend and Tell 리뷰

Show Attend and Tell

들어가기 전에…

이 글을 오후 4시 16분 신촌에서 작성하기 시작했습니다… 오후 3시 무렵부터 논문을 읽기 시작해서 한 시간 남짓 되는 시간 동안 작성한 글이니 아마 문맥도 어색하고, 군데군데 빵꾸가 나있을 가능성이 많고, (아니 빵꾸가 나있을 거고,) 제대로 설명하지 못한 부분도 많을 것 같아요…. 넓은 아량으로 이해해주시면 감사하겠습니다….

Image Captioning

사진을 보고 그 사진에 대한 적절한 문장을 만들어내는 것은 아주 고전적인 문제죠. 이를 위해서는 사진에 어떤 물체가 있는지 찾아내는 것을 넘어, 물체와 물체 사이의 관계를 자연어로 표현할 수도 있어야합니다. 즉 단순한 detect + 단순한 generation의 문제는 아닌 것이죠. 여러 가지 시도들이 있어 왔습니다. Show and Tell이라든지.. 이러한 시도들처럼 Encoder-Decoder의 느낌의 구조는 가져가면서 새로운 방법을 추가했습니다. 그게 바로 attention이구요.

사람이 이미지를 보고 적절한 문장을 만들어낸다고 해봅시다. 과연 사람이 이미지의 모든 부분을 동일하게 중요하다고 인식할까요? 그러니까 새가 날아가는 사진이 있다고 했을 때, 새와 주위 배경 모두 똑같이 중요하다고 생각할까요? 아니겠죠. 중요한 것은 “새”이지 주변의 하늘이나 구름이 아닙니다. 따라서 아마 사람은 “새”에 주목을 할 것입니다. 이러한 관점에서 생각해본다면 이미지에서 특징을 뽑아낸 다음 중요한 부분만을 뽑아내는 attention을 적용하는 것이 합리적으로 보입니다. 실제로 이를 적용했더니 겨과가 더 좋아지기도 했구요. 단순한 Attentoin을 넘어 이 논문에서는 hard attention과 soft attention, 두 가지의 attention을 제안합니다.

Model

그전에 간단하게 모델의 구조부터 짚고 넘어갑시다. 기본적으로 이미지에서 특징을 뽑아내는 Encoder와 이렇게 뽑아낸 특징에서 문장을 생성하는 Decoder로 구분할 수 있습니다. Encoder는 이미지 하나를 받아 $D$차원의 벡터 $\mathbf{a}$를 $L$개 만들어 냅니다. 즉

\[a = \{\mathbf{a}_1, ..., \mathbf{a}_L\}, \mathbf{a}_i \in \mathbb{R}^D\]

입니다. 따라서 CNN을 사용할 때 FC를 사용하지 않고 작은 Conv layer를 사용했다고 하네요.

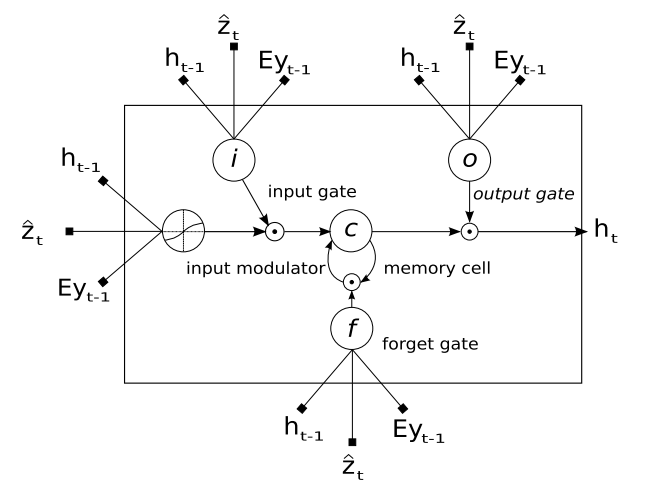
Decoder의 경우에는 LSTM을 사용합니다. 이전에 출력한 단어, 이전의 hidden state, 그리고 context vector $\hat{\mathbf{z}}$를 가지고 연산, 새로운 단어를 만들어내는 작업을 수행하구요. 여기서 $\hat{\mathbf{z}}$가 오늘의 꽃입니다. 주어진 시점 $t$, 즉 $t$번째 단어를 예측할 때 이미지의 어느 부분에 초점을 맞춰야하는지를 나타내 주는 것이죠.

\[\mathbf{e}_{ti} = f_{att}(\mathbf{a}_i, \mathbf{h}_{t-1})\] \[\alpha_{ti} = \frac{exp(e_{ti})}{\sum_{k=1}^L exp(e_{tk})}\]

이고, \(z_t = \phi( \{\mathbf{a}_i\}, \{\alpha_i\})\)라고 나타냅니다. \(\alpha\)는 softmax를 취한 것이므로 $\sum \alpha$는 1이 될 것입니다. 결국 여기서 핵심이 되는 것은 $f_{att}$과 $\phi$이고, 이것에 대한 설명이 이어서 나옵니다.

Hard Attention

(여기서부터는 거의 이해를 하지 못했습니다) Hard Attention은 별도의 Sampling을 통해서 Attention을 뽑아내는 것이고, Smoft Attention은 이러한 Sampling 과정을 근사?하여 End-to-End, 즉 일반적인 Back prop이 가능하게 만들어준 것이라 합니다.

먼저 Hard Attention에 대해서 알아봅시다. 우리가 뽑아내고 싶은 것은 Attention, 즉 인코딩된 이미지 벡터에서 어느 부분에 초점을 맞춰야하는가입니다. 이를 $s_t$라고 해봅시다. $t$번째 단어를 만들때 초점을 맞추는 부분을 의미합니다. 또한 이는 one-hot encoding되어 있는 벡터입니다. 다시말하자면, 우리가 갖고있는 $L$개의 $\mathbf{a}$ 중에서 초점을 맞추고 싶은 부분만 1의 값을 갖는다는 뜻입니다. 식으로 표현하면 $p(s_{t,i}= 1 \lvert s_{j<t}, a) = \alpha_{t, i}$이고 \(\hat{z}_{t} = \sum_{i} {s_{t,i} \mathbf{a}_i}\)가 됩니다.

이때 우리의 목표는, 주어진 $\mathbf{a}$에 대해서 가장 가능성 높은 단어 $y$를 고르는 것입니다. 따라서 $\max({ \log{p(y \lvert a)}})$라는 식을 목적함수로 갖는데요, 딥러닝에서 보통 그렇듯, lower bound를 잡아놓고, 이를 최대화하는 방식을 사용합니다. 이때 잡는 lower bound에는 $s$를 사용하구요. $L_s = \sum_s {p(s \lvert a) \log p(y \lvert s, a)} \le \log p(y \lvert a)$라고 표현합니다. 또한 이를 $W$에 대해 편미분해 gradient descent를 사용할 수도 있습니다. (생략) 하지만 이런 방식의 문제점은 안에 시그마때문에 Gradient를 계산하는 과정에서 많은 시간이 필요하다는 것입니다. 이를 샘플링을 통해서 해결하려고하고, 그냥 적용하면 Variance가 크다는 문제가 있어 이동평균?(Moving average)를 함께 사용합니다… 몬테 카를로 방식을 활용한다는데(Monte Carlo based sampling), 그냥 몬테 카를로도 잘 몰라요ㅜㅜ 죄송합니다. 여튼 이렇게 했더니 강화학습에 사용하는 식과 똑같은 식을 얻을 수 있다고 합니다. 즉 강화학습을 이용해 모델을 학습시킬 수 있게 되는 것이죠.

Soft Attention

Hard Attention의 경우, 일일이 샘플링을 해줘야한다는 문제가 존재합니다. 따라서 이를 일반적인 back prop으로 End-to-End 학습을 가능하게 하기 위해 Soft Attention을 제안합니다. Soft Attention의 경우 $\phi$는 \(\sum_i^L \alpha_i \mathbf{a}_i\)가 됩니다. $s$를 사용하는 대신 확률값을 바로 적용해주는 것이죠. 이렇게 하면 모델이 smooth해지고 differentiable해져 역전파를 사용할 수 있다고 합니다… (기타 과정 생략) 결국 최종 목적함수는 $L_d = -\log(p(y \lvert x)) + \lambda\sum_i^L(1-\sum_t^C{\alpha_{ti}})$가 됩니다.

Result

했더니 좋더라…

Reference

후반의 Attention부분은 이 글을 많이 참조했습니다…